阅读此文前，朦拢您点击一下“关注”骚女qq，既节略您进行磋磨与共享，又给您带来不相同的参与感，感谢您的支援

综述

平行线的倡导深信每个东谈主都能用我方的话语说个或然，毕竟上学的时候都学过。然则你知谈吗，在天才的眼里，平行线冲破了咱们的解析，以致能够相交。

如斯果敢的办法不啻是你我这类凡东谈主难以斡旋，在天才所处的年代亦然惊世震俗。然则跟着本事的推移，他的办法终究被阐扬注解了。这个天才即是咱们今天故事的主角，罗巴切夫斯基。

天才少年的出身

罗巴切夫斯基的出身和门第一直都是一个谜。他的故事始于1792年12月1日，所在是俄罗斯的下诺夫哥罗德，他的父亲是伊万·洛巴切夫斯基，一位从事地盘测量的职员，而母亲则是普拉斯科维娅·洛巴切夫斯卡娅，领有着波兰血缘。

干系词，还有一种说法觉得，罗巴切夫斯基的生身父亲践诺上是谢巴尔申，一位毕业于莫斯科大学的测量师，与罗巴切夫斯基的母亲有着深邃的神气纠葛。

罗巴切夫斯基从小展现出对数学的出色天禀和浓厚意思意思，凭借出色的收成，他在毕业后，胜利参预喀山大学深造。

在喀山大学，罗巴切夫斯基深受德国数学家马丁·巴特尔斯训导的启发，后者曾是高斯的一又友和导师。巴特尔斯对数学有浩瀚的了解，他向罗巴切夫斯基先容了欧几里得几何的基甘心趣和公理，以及尝试阐扬注解平行公设的一些措施。

1811年，罗巴切夫斯基得回了物理和数学的硕士学位。随后，他在1814年景为喀山大学的讲师，在1822年，他荣升为正训导，并担任藏书楼委员会的主席。在此本事，他一直对数学保执着高度的存眷，并进行着我方的相关。

天才的惊东谈主办法

在欧几里得几何规模，存在一条要道公理：在一个平面上，过小数不在一条直线上，只可作出一条与这条直线平行的直线。这即是驰名的平行公设，是欧几里得几何的基石之一。

干系词，罗巴切夫斯基对这个公理建议了质疑，他觉得这个公理并不解显，也不是皆备势必的，应当存在一些迥殊情况不错证伪。他启动尝试拓荒一种不依赖于平行公设的几何体系，也即是双曲几何，其中平行线不错相交于无限远方。

那么，平行线到底是什么呢？在欧几里得几何中，平行线是指长久不相交的两条直线，它们在职何位置都保执讨论的距离。

而在双曲几何中，平行线的界说有所不同，它们是指在归拢个方朝上不相交的两条直线，它们在一侧趋近于相交，而在另一侧则缓缓隔离。罗巴切夫斯基的相关引颈咱们重新想考了平行的倡导，使得数学天下领有了更为广泛的几何不雅念。

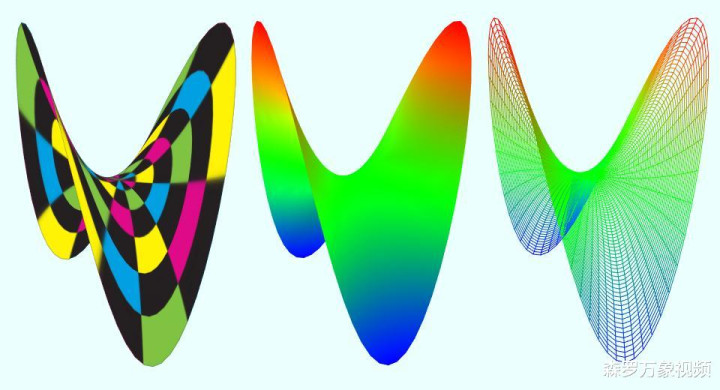
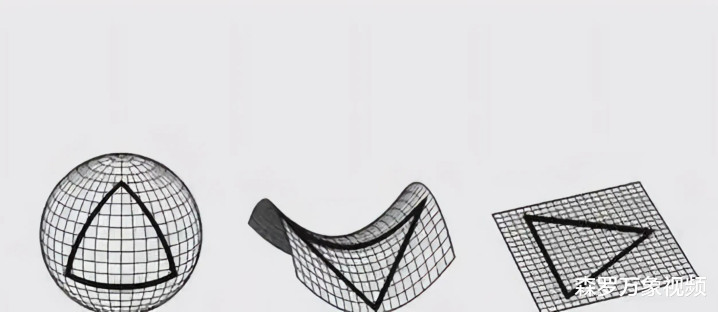
为了更好地敷陈这一倡导，咱们不错借助一个马鞍形状的曲面来模拟双曲平面，这个曲面被数学家称为双曲抛物面。它是一种具有负曲率的曲面，也即是说，在其每小数都是凹下的，就像一个马鞍相同。

在这个曲面上绘画一些直线，咱们会不雅察到一些意思意思意思意思的酣畅。有些直线是不相交的，但它们并非平行，因为在一侧它们缓缓集合，而在另一侧则缓缓分辩，这些直线被称为超平行线。

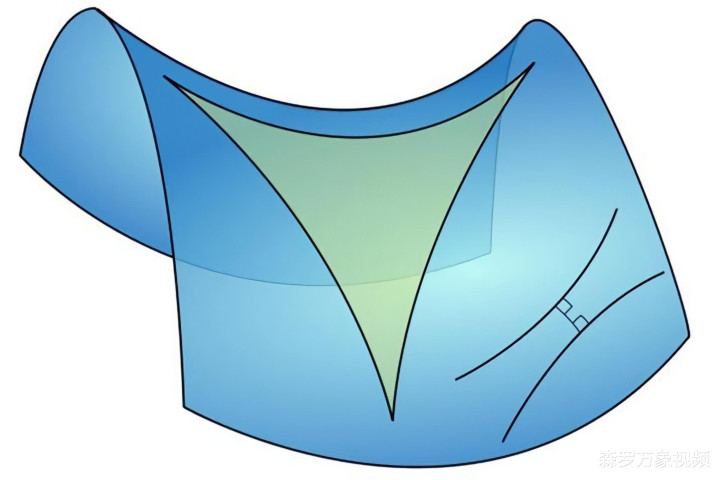
还有些直线是相交但不垂直，这些直线被称为超垂直线。另外，有些直线是平行的，但并不会保执等距，它们在双曲平面的一侧无限接近，而在另一侧无限隔离，这些直线被称为极限平行线。

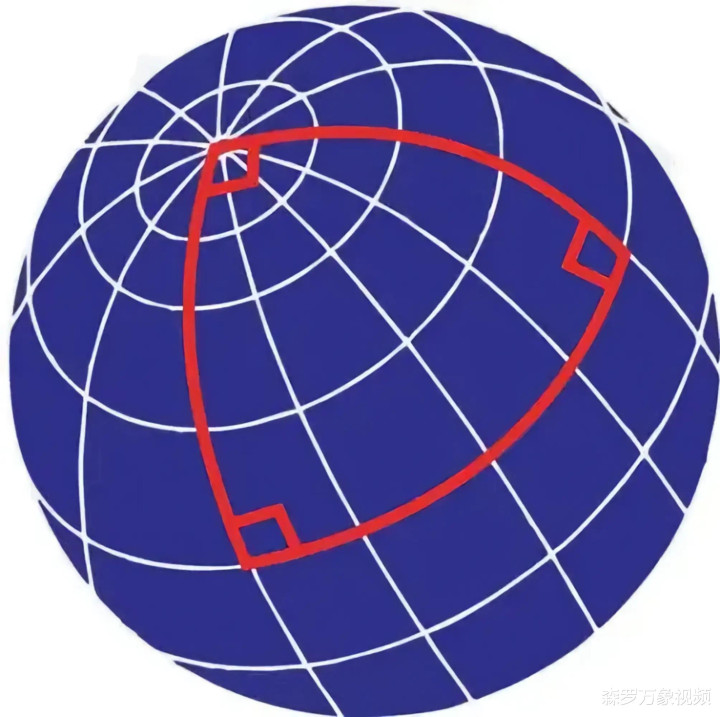
在双曲几何中，通过小数不在一条直线上，咱们能够作出无数条与这条直线平行的直线。这些直线都是极限平行线，它们在归拢个方朝上不相交，但在另一个方朝上却相交于无限远方。

这是罗巴切夫斯基建议的平行线不错相交的表面，与欧几里得几何的平行公设有着骨子的不同。这种表面在19世纪初是一项颠覆性的发现，干系词其时数学界对此进行了哄笑和摒除。

迟来的阐扬注解

尽管罗巴切夫斯基建议了双曲几何的表面，但他未能阐扬注解其一致性，也即是说，他未能阐扬注解双曲几何不会导致矛盾或悖论。他也未能找到一个合适的模子，即找不到一个不错用双曲几何形色的践诺对象或结构。

在其时，罗巴切夫斯基的表面遭到了数学界的忽视和抵赖。他的同业们觉得他的表面是裂缝的，以致是荒诞的。

他的论文在俄国和德国都莫得引起太多关注，他的著述也莫得普通传播。这对他的声誉和地位形成了很大影响，他在1846年被动辞去了喀山大学的校长职务，并于1851年失去了训导头衔。

罗巴切夫斯基于1856年离世，他的表面仍未得到普通招供和确定。干系词，他在墓碑上现时了一句气定神闲的名言：“莫得东谈主能够抹去我的发现。”

这也让东谈主对他对双曲几何的孝敬心生敬意，尽管他在生前未能亲目击证其表面的擢升和给与。干系词，罗巴切夫斯基的表面并未跟着他的离世而消亡，违犯，在他物化后的数十年间，其他数学家阐扬注解了这一表面的正确性和进击性。

最初，罗巴切夫斯基的表面得到了高斯的支援。1846年，高斯收到了罗巴切夫斯基的著述。尽管他莫得实时覆信，但在他于1855年物化后，东谈主们发现了一封他唱和罗巴切夫斯基表面的信，这成为对该表面的进击支援。

其次，波耶也镇静建议了与罗巴切夫斯基讨论的双曲几何表面。波耶是一位匈牙利数学家，他的父亲曾是高斯的学生，于1832年镇静建议了双曲几何的表面。

波耶的论文发表在1832年的一册匈牙利杂志上，但并未引起普通关注。直到1856年，高斯的学生施韦克尔特将波耶的论文翻译成德文，使更巨额学家了解到双曲几何的存在。这一系列的发现缓缓为罗巴切夫斯基的表面赢得了普通招供。

最终，罗巴切夫斯基的表面得到了贝尔特拉米的阐扬注解，贝尔特拉米是一位意大利数学家。他在1868年建议了两个双曲几何的模子，一个是基于圆盘的几何，被称为贝尔特拉米圆盘模子，另一个是基于球面的几何，称为贝尔特拉米伪球面模子。

这两个模子不错用欧几里得几何的措施来形色，但它们的性质妥贴双曲几何的公理，从而阐扬注解了双曲几何的一致性，也即是说，它不会导致矛盾或悖论。贝尔特拉米的模子为双曲几何提供了直不雅的图像，使东谈主们更容易斡旋和给与这一表面。

结语

这些数学家的为罗巴切夫斯基证明了他的表面。双曲的表面对爱因斯坦的相对论和其他科学规模也产生了深切影响。他的表面为东谈主们提供了对几何学的新视角和意志，同期让东谈主们感受到数学的好意思妙和奥秘。

香蕉视频无限次数在线观看视频

临了，由于平台律例，唯有当您跟我有更多互动的时候，才会被认定为铁粉。要是您心爱我的文章骚女qq，不错点个“关注”，成为铁粉后能第一本事收到文章推送。